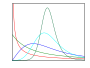
تابع الكثافة الاحتمالية

توقيع صندوقي ودالة الكثافة الاحتمالية (pdf) لتوزيع احتمالي گاوسي N(0, σ²)

في نظرية الاحتمالات، دالة الكثافة الاحتمالية (د.ك.ا) probability density function أو (pdf) هي الدالة الممثلة لأي توزيع احتمالي عن طريق التكامل. وتكون دالة الكثافة الاحتمالية موجبة دائمًا، كما ويكون تكاملها من ∞- إلى ∞+ مساويًا لواحد:

${\displaystyle{\displaystyle\int_{-\infty}^{+\infty}f\left(x\right)dx=1}}$

يمكن وصف دالة الكثافة الاحتمالية بأنها عبارة عن تقويم لاستمرارية منسّج(أي Histogram) الذي يمثل التكرارات النسبية ضمن مجالات النتائج البيانية.

 توزيعات مستمرة بمتغير واحد

تكون للمتغير العشوائي ${\displaystyle{\displaystyle X}}$ دالة كثافة إحتمالية ${\displaystyle{\displaystyle f\left(X\right)}}$، حيث قيم هذه الدالة غير سالبة وهي قابلة للتكامل حسب ليبيغ، إذا ما تحقّق :

${\displaystyle{\displaystyle P\left[a\leq X\leq b\right]=\int_{a}^{b}f\left(x\right)dx}}$

أي أنّ الاحتمال بأن يتخذ المتغير ${\displaystyle{\displaystyle X}}$ قيمًا في الفترة ${\displaystyle{\displaystyle\left[a,b\right]}}$ مساوية لتكامل دالة الكثافة الاحتمالية في نفس الفترة. من هنا، فإذا كانت ${\displaystyle{\displaystyle F}}$ هي دالة التوزيع التراكمي للمتغير ${\displaystyle{\displaystyle X}}$، يتحقق:

${\displaystyle{\displaystyle,F\left(x\right)=\int_{-\infty}^{x}f\left(u\right)du}}$

وكذلك، فإنّ:

${\displaystyle{\displaystyle f\left(x\right)={\frac{d}{dx}}F\left(x\right)}}$

من هنا، فإذا كان لدينا توزريعًا احتماليًا له كثافة ${\displaystyle{\displaystyle f\left(x\right)}}$, عندئذ يكون الاحتمال للحصول على قيم في المجال اللامتناهي ${\displaystyle{\displaystyle\left[x,x+dx\right]}}$ هو ${\displaystyle{\displaystyle f\left(x\right)dx}}$.

 دوال كثافة احتمالية مهمة

• التوزيع المنتظم هو أحد أكثر التوزيعات أهمية واستعمالاً. في صيغته المستمرة نقول أنّ للمتغير العشوائي X توزيعًا منتظمًا في الفترة ${\displaystyle{\displaystyle\left[a,b\right]}}$ إذا كان احتمال حصول X على قيمة ما في فترة جزئية محتواة في الفترة ${\displaystyle{\displaystyle\left[a,b\right]}}$ مساويًا لاحتمال حصوله على قيمة ما في فترة جزئية أخرى محتواة في الفترة ${\displaystyle{\displaystyle\left[a,b\right]}}$، بشرط أن تكون الفترتان بنفس الطول. هذا يقضي بأن يكون لـX نفس الكثافة الاحتمالية على طول الفترة ${\displaystyle{\displaystyle\left[a,b\right]}}$، أي:

${\displaystyle{\displaystyle f\left(x\right)={\begin{cases}{\frac{1}{b-a}}\quad a\leq x\leq b\\ 0\quad\quad x<a,x>b\end{cases}}}}$

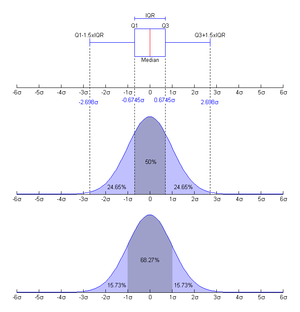
• بالنسبة للتوزيع الاحتمالي الطبيعي أو الغاوسي، فإنّ دالة الكثافة الاحتمالية هي:

${\displaystyle{\displaystyle f\left(x\right)={\frac{1}{\sqrt{2\pi}}}e^{-{\frac{x^{2}}{2}}}}}$

هذا في حالة كون المتغير العشوائي تابع لتوزيع طبيعي معياري، أي أنّه ذو قيمة متوقّعة مساوية لصفر، وتباين مساوٍ لواحد. أمّا إذا كانت القيمة المتوقّعة مساوية لـ-${\displaystyle{\displaystyle\mu}}$ والتباين مساويًا لـ-${\displaystyle{\displaystyle\sigma^{2}}}$ تكتب دالة الكثافة الاحتمالية كالتالي:

${\displaystyle{\displaystyle f\left(x\right)={\frac{1}{\sqrt{2\pi\sigma^{2}}}}e^{-{\frac{\left(x-\mu\right)^{2}}{2\sigma^{2}}}}}}$

 استعمالات

• حساب القيمة المتوقعة لمتغير عشوائي ما يتم وفق المعادلة التالية:

${\displaystyle{\displaystyle E\left[X\right]=\int_{-\infty}^{+\infty}xf\left(x\right)dx}}$

أي أنّ القيمة المتوقعة لمتغيّر عشوائي هي عبارة عن مركز ثقل دالة الكثافة الاحتمالية خاصته.

 انظر أيضًا

• دالة توزيع تراكمي
• دالة الإمكان
• دالة مولدة عزم

 وصلات خارجية

• Eric W. Weisstein, تابع الكثافة الاحتمالية at MathWorld.