شريط موبيوس
(تم التحويل من Möbius strip)

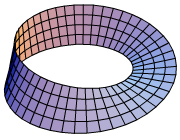
A Möbius strip made with a piece of paper and tape. If an ant were to crawl along the length of this strip, it would return to its starting point having traversed both sides of the strip, without ever crossing an edge.
شريط موبيوس أنشوطة (عقدة) متصلة، بها نصف جَدْلَة. ويمكنك صنع شريط موبيوس، بأخذ شريط ورق مستطيل وقلب أحد طرفيه (ليّه) 180° وضم الطرفين. وبالرغم من أن الشريط كان ثنائي الجانبين، إلا أن شريط موبيوس له جانب واحد. ولمراجعة ذلك، قم برسم خط أسفل وسط الشريط إلى أن تصل إلى النقطة التي بدأت منها. وسوف تكتشف أن الخط يمر حول كلا جانبي الشريط. وعلى نحو مماثل، فإن لشريط موبيوس حافة واحدة. فإذا مررت أصبعك على طول حافته، فإنك ستعود إلى نقطة انطلاقك بعد مرورك حول الحافة بأكملها. وإذا قطعت الشريط إلى جزئين على طول الخط الذي رسمته، فإنه سيبقى أنشوطة واحدة، لكن لها جانبان. وقد سُمِّي شريط موبيوس باسم أوغست فيردناد موبيوس، عالم الرياضيات الألماني الذي اكتشفه في أواسط القرن التاسع عشر الميلادي.
الهندسة والطوبولوجيا
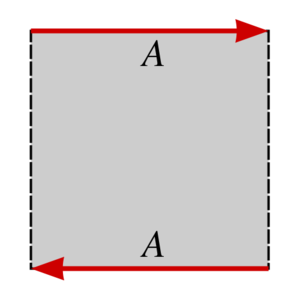
لتحول مستطيل إلى شريط موبيوس، صِل الحافتين المسماتين A بحيث أن اتجاهات الأسهم تتماثل.
الحدوث والاستخدامات في الطبيعة والتكنولوجيا

وشاح مصمم كشريط موبيوس.

رمز التدوير العالمي كأحد أشكال شريط موبيوس.
انظر أيضاً
- أوگوست فرديناند موبيوس
- Cross-cap
- List of cycles
- Loop
- M.C. Escher
- Molecular knot
- Paradox
- Real projective plane
- Strange loop
- Umbilic torus
المصادر
وصلات خارجية
مشاع المعرفة فيه ميديا متعلقة بموضوع [[commons: Category:Moebius surfaces
| Moebius surfaces
]].- A virtual walk in the solar wind
- Animation of a rotating Sudanese Möbius band
- Louis Buckley (2007-07-15). "Möbius strip unravelled". Nature. doi:10.1038/news070709-16. Retrieved 2006-07-16.
- h2g2 - The Amazing Möbius Strip
- Johann Benedict Listing
- Knitted version
- Möbius strip at cut-the-knot
- Science News 7/28/07: A Twist on the Möbius Band: Researchers work out the shape of a paper strip
- The Möbius Gear — A functional planetary gear model in which one gear is a Möbius strip
- Visualization of J. S. Bach's crab canon on a Möbius strip
- The protein with a topological twist
- Tridimensional and rotational möbius strip
- Eric W. Weisstein, Möbius Strip at MathWorld.
This article contains content from Wikimedia licensed under CC BY-SA 4.0. Please comply with the license terms.