مدار

مدار جسم ثانوي يدور حول جسم أساسي يمكن أن يكون قطعًا ناقصًا أو قطعًا مكافئًا أو قطعًا زائدًا، كما هو مبين في المخطط أعلاه. يتحدد الشكل حسب سرعة الجسم الثانوي وصلتها بالسرعة المطلوبة للتحرر من الجسم الأساسي.

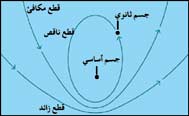
المدار Orbit مسار الجسم الطبيعي أو الصناعي الذي يتحرك بتأثير قوة مركزية. ويعني مصطلح المدار في علم الفلك بصورة محددة مسار أي جسم تكون حركته تحت سيطرة شدّ جاذبية جسم آخر. ويسمي علماء الفلك الجسم الأضخم الأساسي والجسم الأقل ضخامة الثانوي. فالقمر مثلاً هو الثانوي الذي يدور في فلك الجسم الأساسي وهو الأرض. والأرض بدورها ثانوي يدور حول الأساسي وهو الشمس. ويمكن لسفن الفضاء أن تصبح ثانويات للأرض أو أي كوكب آخر، أو توابع للقمر والشمس.

Two bodies with a slight difference in mass orbiting around a common barycenter. The sizes, and this particular type of orbit are similar to the Pluto-Charon system.

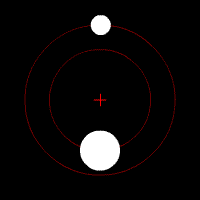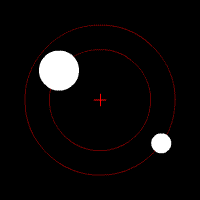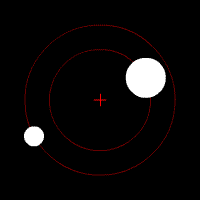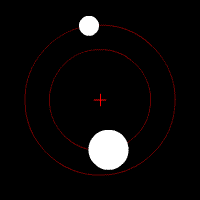
ومدار الجسم الثانوي ضمن تأثير جاذبية الجسم الأساسي هو قوس مغلق يُدعى القطع الناقص. والمدارات الدائرية الكاملة نادرة الحدوث. وفي المدارات الإهليلجية الشكل لا يكون الجسم الأساسي في مركز القطع الناقص. ونتيجة لذلك يقترب الثانوي من الأساسي في بعض الأحيان أكثر مما يقترب في أحيان أخرى. وتدعى النقطة التي يكون فيها الثانوي التابع للأرض أقرب ما يكون منها في المدار الحضيض أما أبعد نقطة فتدعى الأوج. وبالنسبة للثانوي التابع للشمس تدعى أقرب نقطة في المدار نقطة الرأس وأبعد نقطة نقطة الذنب.

يمكن للجسم الثانوي أن يكتسب سرعة كافية كي يهرب من تأثير جاذبية الجسم الأساسي. فإذا حقق سرعة الانفلات هذه، يصبح مداره قوسًا مفتوحًا يدعى القطع المكافئ. وإذا تحرك الجسم الثانوي بأسرع من سرعة الانفلات، يصبح مداره قوسًا أكثر انفتاحًا يدعى القطع الزائد. وسفينة الفضاء التي تغادر مدارها حول الأرض تبدأ الدوران على مدار ذي قطع زائد. تنطلق سفينة الفضاء إلى كواكب أخرى داخل المجموعة الشمسية مستخدمة مسارات الجاذبية المساعدة. يتعدل المدار في كل مرة تقترب فيها سفينة الفضاء من الكوكب. وأثناء الاجتياز العابر يحرف شدّ الجاذبية سفينة الفضاء ويوجهها نحو الكوكب الآخر الذي ستزوره. وقد استخدم المسبار الفضائي فويجر2 مسار الجاذبية المساعد، لزيارة أربعة كواكب. فقد زار المسبار المُشتري في عام 1979م، ثم حرفه مجال جاذبيته نحو كوكب زُحل الذي وصل إليه في عام 1980م. ووجّه زحل بدوره المسبار الفضائي نحو أورانوس الذي وصله عام 1986م. وحرف أورانوس المسبار باتجاه نبتون الذي وصل إليه في عام 1989م.

 الاضطرابات

المقالة الرئيسية: اضطراب (فلك)

للمزيد من المعلومات: Osculating orbit § Perturbations, and Orbit modeling § Perturbations

An orbital perturbation is when a force or impulse which is much smaller than the overall force or average impulse of the main gravitating body and which is external to the two orbiting bodies causes an acceleration, which changes the parameters of the orbit over time.

 الاضطرابات الشعاعية والتقدمية والعرضية

A small radial impulse given to a body in orbit changes the eccentricity, but not the orbital period (to first order). A prograde or retrograde impulse (i.e. an impulse applied along the orbital motion) changes both the eccentricity and the orbital period. Notably, a prograde impulse at periapsis raises the altitude at apoapsis, and vice versa and a retrograde impulse does the opposite. A transverse impulse (out of the orbital plane) causes rotation of the orbital plane without changing the period or eccentricity. In all instances, a closed orbit will still intersect the perturbation point.

 الاضمحلال المداري

المقالة الرئيسية: اضمحلال مداري

If an orbit is about a planetary body with a significant atmosphere, its orbit can decay because of drag. Particularly at each periapsis, the object experiences atmospheric drag, losing energy. Each time, the orbit grows less eccentric (more circular) because the object loses kinetic energy precisely when that energy is at its maximum. This is similar to the effect of slowing a pendulum at its lowest point; the highest point of the pendulum's swing becomes lower. With each successive slowing more of the orbit's path is affected by the atmosphere and the effect becomes more pronounced. Eventually, the effect becomes so great that the maximum kinetic energy is not enough to return the orbit above the limits of the atmospheric drag effect. When this happens the body will rapidly spiral down and intersect the central body.

The bounds of an atmosphere vary wildly. During a solar maximum, the Earth's atmosphere causes drag up to a hundred kilometres higher than during a solar minimum.

Some satellites with long conductive tethers can also experience orbital decay because of electromagnetic drag from the Earth's magnetic field. As the wire cuts the magnetic field it acts as a generator, moving electrons from one end to the other. The orbital energy is converted to heat in the wire.

Orbits can be artificially influenced through the use of rocket engines which change the kinetic energy of the body at some point in its path. This is the conversion of chemical or electrical energy to kinetic energy. In this way changes in the orbit shape or orientation can be facilitated.

Another method of artificially influencing an orbit is through the use of solar sails or magnetic sails. These forms of propulsion require no propellant or energy input other than that of the Sun, and so can be used indefinitely. See statite for one such proposed use.

Orbital decay can occur due to tidal forces for objects below the synchronous orbit for the body they're orbiting. The gravity of the orbiting object raises tidal bulges in the primary, and since below the synchronous orbit, the orbiting object is moving faster than the body's surface the bulges lag a short angle behind it. The gravity of the bulges is slightly off of the primary-satellite axis and thus has a component along with the satellite's motion. The near bulge slows the object more than the far bulge speeds it up, and as a result, the orbit decays. Conversely, the gravity of the satellite on the bulges applies torque on the primary and speeds up its rotation. Artificial satellites are too small to have an appreciable tidal effect on the planets they orbit, but several moons in the Solar System are undergoing orbital decay by this mechanism. Mars' innermost moon Phobos is a prime example and is expected to either impact Mars' surface or break up into a ring within 50 million years.

Orbits can decay via the emission of gravitational waves. This mechanism is extremely weak for most stellar objects, only becoming significant in cases where there is a combination of extreme mass and extreme acceleration, such as with black holes or neutron stars that are orbiting each other closely.

 التفلطح

The standard analysis of orbiting bodies assumes that all bodies consist of uniform spheres, or more generally, concentric shells each of uniform density. It can be shown that such bodies are gravitationally equivalent to point sources.

However, in the real world, many bodies rotate, and this introduces التفلطح and distorts the gravity field, and gives a quadrupole moment to the gravitational field which is significant at distances comparable to the radius of the body. In the general case, the gravitational potential of a rotating body such as, e.g., a planet is usually expanded in multipoles accounting for the departures of it from spherical symmetry. From the point of view of satellite dynamics, of particular relevance are the so-called even zonal harmonic coefficients, or even zonals, since they induce secular orbital perturbations which are cumulative over time spans longer than the orbital period. They do depend on the orientation of the body's symmetry axis in the space, affecting, in general, the whole orbit, with the exception of the semimajor axis.

 الأجرام متعددة الجاذبية

المقالة الرئيسية: مسألة ن من الأجسام

The effects of other gravitating bodies can be significant. For example, the orbit of the Moon cannot be accurately described without allowing for the action of the Sun's gravity as well as the Earth's. One approximate result is that bodies will usually have reasonably stable orbits around a heavier planet or moon, in spite of these perturbations, provided they are orbiting well within the heavier body's Hill sphere.

When there are more than two gravitating bodies it is referred to as an n-body problem. Most n-body problems have no closed form solution, although some special cases have been formulated.

 الإشعاع الخفيف والرياح النجمية

For smaller bodies particularly, light and stellar wind can cause significant perturbations to the attitude and direction of motion of the body, and over time can be significant. Of the planetary bodies, the motion of asteroids is particularly affected over large periods when the asteroids are rotating relative to the Sun.

 مدارات غريبة

Mathematicians have discovered that it is possible in principle to have multiple bodies in non-elliptical orbits that repeat periodically, although most such orbits are not stable regarding small perturbations in mass, position, or velocity. However, some special stable cases have been identified, including a planar figure-eight orbit occupied by three moving bodies. Further studies have discovered that nonplanar orbits are also possible, including one involving 12 masses moving in 4 roughly circular, interlocking orbits topologically equivalent to the edges of a cuboctahedron.

Finding such orbits naturally occurring in the universe is thought to be extremely unlikely, because of the improbability of the required conditions occurring by chance.

 انظر أيضاً

ابحث عن مدار في
قاموس المعرفة.

• Artificial satellite orbit
• Escape velocity
• Gravity
• Kepler orbit
• Kepler's laws of planetary motion
• Molniya orbit
• Orbit (dynamics)
• Orbital spaceflight/Sub-orbital spaceflight
• Perifocal coordinate system
• Rosetta (orbit)
• Trajectory, Hyperbolic trajectory and Parabolic trajectory

 وصلات خارجية

• CalcTool: Orbital period of a planet calculator. Has wide choice of units. Requires Javascript.
• Browser Based Three Dimension Simulation of Orbital Motion. Objects and distance are drawn to scale. Run on Javascript-enabled browser such as Internet Explorer, Mozilla Firefox and Opera.
• Java simulation on orbital motion. Requires Java.
• NOAA page on Climate Forcing Data includes (calculated) data on Earth orbit variations over the last 50 million years and for the coming 20 million years
• On-line orbit plotter. Requires Javascript.
• Orbital Mechanics (Rocket and Space Technology)
• Orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for Earth orbit eccentricity, and also a series for orbital inclination. Orbits for the other planets were also calculated, but only the eccentricity data for Earth and Mercury are available online.
• Understand orbits using direct manipulation. Requires Javascript and Macromedia
• Linton, Christopher (2004). From Exodus to Einstein. Cambridge: University Press. ISBN 0521827507
• Swetz, Frank; et al. (1997). Learn from the Masters!. Mathematical Association of America. ISBN 0883857030

 المصادر

الموسوعة المعرفية الشاملة

• Abell, Morrison, and Wolff (1987). Exploration of the Universe (fifth edition ed.). Saunders College Publishing. {{cite book}}: |edition= has extra text (help)CS1 maint: multiple names: authors list (link)