خوارزمية شور

خوارزمية شوور هي خوارزمية كنتيكية ل التفكيك لعدد طبيعي N في زمن O((log N)³) و في مساحة O(log N), تحمل اسم پيتر شور.

 العمليات

ليكن N عدد طبيعي معطى ، نحاول إيجاد عدد آخر p محصور بين 1 و N و يقسم N.

خوارزمية شوور مقسمة إلى قسمين :

1. اختصار مشكلة التفكيك إلى مشكلة الترتيب (نظرية المجموعات), و التي يمكن تطبيقها باستعمال حاسوب عادي.
2. خوارزمية كانتيكية لحل مشكلة البحث عن الدور.

 المرحلة الكلاسيكية

1. أخد عدد شبه عشوائي a < N
2. حساب pgcd(a, N). و التي يمكن ايجادها باستعمال خوارزمية اقليدس.
3. إذا كان pgcd(a, N) ≠ 1, إذن سيكون قاسما فعليا N, يعني نهاية الخوارزمية.
4. و ألا, استعمال البحث عن الدور (انظر أسفله) لإيجاد r, دالة دورية للدالة الآتية :
   ${\displaystyle{\displaystyle f(x)=a^{x}\ {\mbox{mod}}\ N}}$,
   يعني. أصغر عدد صحيح طبيعي r بحيث ${\displaystyle{\displaystyle f(x+r)=f(x)}}$.
5. إذا كان r فردي, نعود للمرحلة 1 1.
6. إذا كان a ^r/2 ≡ -1 [N], نعود للمرحلة 1.
7. قواسم N هي pgcd(a^r/2 ± 1, N). انتهى.

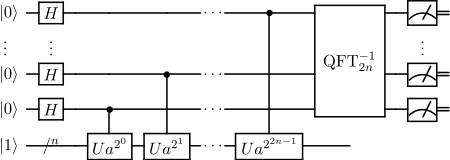
 Quantum part: period-finding subroutine

Quantum subroutine in Shor's algorithm

 اقرأ أيضاً

• خوارزمية گروڤر
• تحليل (رياضيات)
• فيزياء رياضية

 وصلات خارجية

• Version 1.0.0 of libquantum: contains a C language implementation of Shor's algorithm with their simulated quantum computer library, but the width variable in shor.c should be set to 1 to improve the runtime complexity.
• PBS Infinite Series created two videos explaining the math behind Shor's algorithm, "How to Break Cryptography" and "Hacking at Quantum Speed with Shor's Algorithm".