في الهندسة الرياضية، التحويل الأفيني بين فضائين شعاعيين (أو بشكل دقيق فضائين أفينيين) يتكون من تحويل خطي يتبع بعملية نقل:

(أصل كلمة أفين هي من اللغة اللاتينية affinis وتعني "المتصل").
في البعد الأفيني، كل تحويل أفيني يعطى بالمصفوفة A والمتجهة b .
بالمعنى الفيزيائي، التحويل الأفيني هو التحويل الذي يحافظ على:
- العلاقة الخطية بين النقاط، أي أن أي ثلاث نقاط واقعة على مستقيم واحد تبقى واقعة على مستقيم بعد التحويل
- النسب على طول المستقيم، أي من أجل ثلاث نقاط
 ,
,  ,
,  تقع على مستقيم، فإن النسبة
تقع على مستقيم، فإن النسبة  تكون محققة قبل وبعد التحويل.
تكون محققة قبل وبعد التحويل.
التعريف الرياضي
الراسم الأفيني  بين فضائين أفينيين هو راسم يعمل على متجهات، معرفة بأزواج من النقاط، كـتحويل خطي: يوجد تحويل خطي φ بحيث
بين فضائين أفينيين هو راسم يعمل على متجهات، معرفة بأزواج من النقاط، كـتحويل خطي: يوجد تحويل خطي φ بحيث

for any pair of points  . If an origin
. If an origin  is chosen, and
is chosen, and  denotes its image
denotes its image  , then this means that for any vector
, then this means that for any vector  :
:

If an origin  is also chosen, this can be decomposed as an affine transformation
is also chosen, this can be decomposed as an affine transformation  that sends
that sends  , namely
, namely

followed by the translation by a vector  .
.
تحويلات أفينية في الهندسة المستوية
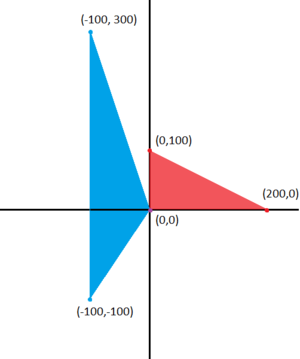
A simple affine transformation on the real plane
في ℝ2, the transformation shown at right is accomplished using the map given by:

انظر أيضاً
الهامش




















