ثابت أفوجادرو

Avogadro constant
Avogadro constant
	Amedeo Avogadro, the constant's namesake
Common symbols	NA, L
SI unit	mol−1
Exact value
reciprocal mole	6.02214129(27)×1023

كمية المادة من أي عنصر تساوي الرقم الدال على كتلته الذرية مقدرا بالغرام تحتوي على عدد من الذرات لا يتغير من عنصر لآخر يدعى عدد (رقم) أفوجادرو. وهو يساوي إلى 6.022 × 10²³ فمثلا: عدد الذرات الموجودة في 27 غ من الألومنيوم = عدد الذرات الموجودة في 108 غ من الفضة = 6.022 × 10²³ لأن 27 هي الكتلة الذرية للألمنيوم و 108 الكتلة الذرية للفضة.

عدد/رقم/ثابت أفوغادرو نسبة إلى العالم الإيطالي Amadio Avogadro

The Avogadro constant is used as a proportionality factor in relating the amount of substance $n (X)$ , in a sample of a substance $X$ , to the corresponding number of elementary entities $N (X)$ :

{\displaystyle{\displaystyle n(\mathrm{X})={\frac{N(\mathrm{X})}{N_{\mathrm{A}% }}}}}

The Avogadro constant $N A$ is also the factor that converts the average mass $m (X)$ of one particle of a substance to its molar mass $M (X)$ .^[1] That is, $M (X) = m (X) \cdot N A$ . Applying this equation to ¹²C with an atomic mass of exactly 12 Da and a molar mass of 12 g/mol yields (after rearrangement) the following relation for the Avogadro constant: $N A$ = (g/Da) mol⁻¹, making the Avogadro number $N 0$ = g/Da. Historically, this was precisely true, but since the 2019 revision of the SI, the relation is now merely approximate, although equality may still be assumed with high accuracy.

The constant $N A$ also relates the molar volume (the volume per mole) of a substance to the average volume nominally occupied by one of its particles, when both are expressed in the same units of volume. For example, since the molar volume of water in ordinary conditions is about 18 mL/mol, the volume occupied by one molecule of water is about 18/(6.022×10²³) mL, or about 0.030 nm³ (cubic nanometres). For a crystalline substance, $N 0$ relates the volume of a crystal with one mole worth of repeating unit cells, to the volume of a single cell (both in the same units).

Definition

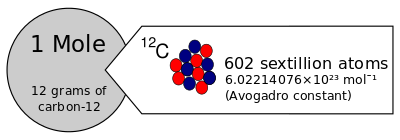
Approximate definition of a mole based on 12 grams of carbon-12

The Avogadro constant was historically derived from the old definition of the mole as the amount of substance in 12 grams of carbon-12 (¹²C). By this old definition, the numerical value of the Avogadro constant in mol⁻¹ (the Avogadro number) was a physical constant that had to be determined experimentally.

The historical relationship of the Avogadro constant to the molar mass of carbon-12, $M (12 C)$ , and its atomic mass, $m (12 C)$ , can be expressed in the following equation:

{\displaystyle N_{\text{A}}={\frac{M(^{12}{\text{C}})}{m(^{12}{\text{C}})}}={% \frac{12{\text{ g/mol}}}{12{\text{ Da}}}}={\frac{\text{g/mol}}{\text{Da}}}=({% \text{g/Da}}){\text{ mol}}^{-1}}

Thus, $N 0$ , the numerical value of $N A$ , was equal to the number of daltons in a gram (g/Da), where the dalton is defined as 1/12 of the mass of a ¹²C atom.^[2]

The redefinition of the mole in 2019, as being the amount of substance consisting of exactly 6.02214076×10²³ elementary entities,^[3] means that the mass of 1 mole of a substance is now exactly the product of the Avogadro number and the average mass of one of the entities involved. The dalton, however, is still defined as 1/12 of the mass of a ¹²C atom, which must be determined experimentally and is known only with finite accuracy. Thus, prior experiments that aimed to determine the numerical value of the Avogadro constant when expressed in reciprocal moles—i.e. the Avogadro number (now numerically fixed)—are re-interpreted as measurements of the numerical value in grams of the dalton.

By the old definition of mole, the numerical value of the mass of one mole of a substance expressed in grams (i.e., its molar mass in g/mol or kg/kmol), was precisely equal to the average mass of one particle expressed in daltons. With the new definition, this numerical equivalence is no longer exact, as it is affected by the uncertainty in the value of the gram-to-dalton (g/Da) mass-unit ratio. However, it may still be assumed for all practical purposes. For example, the average mass of one molecule of water is about 18.0153 daltons, and an amount of one mole of water has a corresponding macroscopic mass of about 18.0153 grams. Also, the Avogadro number is the approximate number of nucleons (protons and neutrons) in one gram of ordinary matter.

An amount of substance consisting of just a single elementary entity might be thought of as an "elementary amount", analogous to the elementary charge, $e$ . Letting $n a$ denote this elementary amount, then 1 mol = $N 0 n a$ , with the mole defined such that $N A = N 0$ /mol, which can be rearranged as 1 mol = $N 0 / N A$ . Thus, $n a = 1/ N A$ , the reciprocal of the Avogadro constant. The fundamental definition of the Avogadro constant itself is therefore one per elementary amount ( $N A = 1/ n a$ ), independent of any macroscopic base unit chosen for the physical quantity. (Since there is an aggregate of an Avogadro number of elementary entities in one mole, the Avogadro constant can also be expressed (in terms of the mole) as an Avogadro number per mole—but this is not its "definition".) The Avogadro constant, a well-defined quantity value (with dimension 1/N), independent of the mole, is therefore a bona fide defining constant for the 2019 redefinition of the mole.

Introducing $n a$ in place of $1/ N A$ , means that $n (X) = N (X) n a$ —amount of substance is an aggregate of $N (X)$ elementary entities—which is easier to comprehend than $N (X)$ "reciprocal Avogadro constants". Also the molar mass is then $M (X) = m (X)/ n a$ —the entity mass per entity, which is self-evident.

In older literature, the Avogadro number was also denoted $N$ ,^[4]^[5] although that conflicts with the symbol for number of particles in statistical mechanics.

التاريخ

أصل المفهوم

جان پران في 1926

The Avogadro constant is named after the Italian scientist Amedeo Avogadro (1776–1856), who, in 1811, first proposed that the volume of a gas (at a given pressure and temperature) is proportional to the number of atoms or molecules regardless of the nature of the gas.^[6]

Avogadro's hypothesis was popularized four years after his death by Stanislao Cannizzaro, who advocated Avogadro's work at the Karlsruhe Congress in 1860.^[7]

The name Avogadro's number was coined in 1909 by the physicist Jean Perrin, who defined it as the number of molecules in exactly 32 grams of oxygen gas.^[8] The goal of this definition was to make the mass of a mole of a substance, in grams, be numerically equal to the mass of one molecule relative to the mass of the hydrogen atom; which, because of the law of definite proportions, was the natural unit of atomic mass, and was assumed to be 1/16 of the atomic mass of oxygen.

أول قياسات

Josef Loschmidt

The value of Avogadro's number (not yet known by that name) was first obtained indirectly by Josef Loschmidt in 1865, by estimating the number of particles in a given volume of gas.^[9] This value, the number density $n 0$ of particles in an ideal gas, is now called the Loschmidt constant in his honor, and is related to the Avogadro constant, $N A$ , by

{\displaystyle{\displaystyle n_{0}={\frac{p_{0}N_{\rm{A}}}{R\,T_{0}}},}}

where $p 0$ is the pressure, $R$ is the gas constant, and $T 0$ is the absolute temperature. Because of this work, the symbol $L$ is sometimes used for the Avogadro constant,^[10]^[11] and, in German literature, that name may be used for both constants, distinguished only by the units of measurement.^[12] (However, $N A$ should not be confused with the entirely different Loschmidt constant in English-language literature.)

Perrin himself determined the Avogadro number, which he called "Avogadro's constant" (constante d'Avogadro), by several different experimental methods. He was awarded the 1926 Nobel Prize in Physics, largely for this work.^[13]

The electric charge per mole of electrons is a constant called the Faraday constant and has been known since 1834, when Michael Faraday published his works on electrolysis. In 1910, Robert Millikan with the help of Harvey Fletcher obtained the first measurement of the charge on an electron. Dividing the charge on a mole of electrons by the charge on a single electron provided a more accurate estimate of the Avogadro number.^[14]

إعادة تعريف النظام المتري في 1971

In 1971, in its 14th conference, the International Bureau of Weights and Measures (BIPM) decided to regard the amount of substance as an independent dimension of measurement, with the mole as its base unit in the International System of Units (SI).^[10] Specifically, the mole was defined as the amount of a substance that contains as many elementary entities as there are atoms in 12 grams (0.012 kilograms) of carbon-12 (¹²C).^[2] Thus, in particular, an amount of one mole of carbon 12 had a corresponding mass that was exactly 12 grams of that element.

By this definition, one mole of any substance contained exactly as many elementary entities as one mole of any other substance. However, this number $N 0$ was a physical constant that had to be experimentally determined since it depended on the mass (in grams) of one atom of ¹²C, and therefore, it was known only to a limited number of decimal digits.^[10] The common rule of thumb that "one gram of matter contains $N 0$ nucleons" was exact for carbon-12, but slightly inexact for other elements and isotopes.

In the same conference, the BIPM also named $N A$ (the factor that related the amount of a substance to the corresponding number of particles) the "Avogadro constant". However, the term "Avogadro number" continued to be used, especially in introductory works.^[15] As a consequence of this definition, $N A$ was not a pure number, but had the quantity dimension of reciprocal of amount of substance (N⁻¹).

إعادة تعريف النظام المتري في 2019

In its 26th Conference, the BIPM adopted a different approach: effective 20 May 2019, it defined the Avogadro constant $N A$ as the exact value 6.02214076×10²³ mol⁻¹, thus redefining the mole as exactly 6.02214076×10²³ constituent particles of the substance under consideration.^[16]^[3] One consequence of this change is that the mass of a mole of ¹²C atoms is no longer exactly 0.012 kg. On the other hand, the dalton, Da (a.k.a. unified atomic mass unit, u), remains unchanged as 1/12 of the mass of ¹²C.^[17]^[18] Thus, the molar mass constant remains very close to but no longer exactly equal to 1 g/mol, although the difference (4.5×10⁻¹⁰ in relative terms, as of March 2019) is insignificant for all practical purposes.^[3]^[19]

الصلة بثوابت أخرى

The Avogadro constant $N A$ is related to other physical constants and properties.

It relates the molar gas constant $R$ and the Boltzmann constant $k B$ , which in the SI is defined to be exactly 1.380649×10⁻²³ J/K:^[3]
$R = k B N A =$ 8.3144621(75)×10⁻⁷ J mol⁻¹ K⁻¹
It relates the Faraday constant $F$ and the elementary charge $e$ , which in the SI is defined as exactly 1.602176634×10⁻¹⁹ coulombs:^[3]
$F = e N A =$ 96485.3365(21) C/mol
It relates the molar mass constant $M u$ and the atomic mass constant $m u$ currently 1.660538921(73)×10⁻²⁷ kg:^[20]
$M u = m u N A =$

انظر أيضاً

المراجع

^ Okun, Lev B.; Lee, A. G. (1985). Particle Physics: The Quest for the Substance of Substance. OPA Ltd. p. 86. ISBN 978-3-7186-0228-5.
^ ^أ ^ب قالب:SIbrochure8th
^ ^أ ^ب ^ت ^ث ^ج David B. Newell and Eite Tiesinga (2019): The International System of Units (SI). NIST Special Publication 330, National Institute of Standards and Technology. DOI:10.6028/nist.sp.330-2019 قالب:S2cid
^ Linus Pauling (1970), General Chemistry, p. 96. Dover Edition, reprinted by Courier in 2014; 992 pages. ISBN 978-0486134659
^ Marvin Yelles (1971): McGraw-Hill Encyclopedia of Science and Technology, Vol. 9, 3rd ed.; 707 pages. ISBN 978-0070797987
^ Avogadro, Amedeo (1811). "Essai d'une maniere de determiner les masses relatives des molecules elementaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons". Journal de Physique. 73: 58–76. English translation.
^ "Stanislao Cannizzaro | Science History Institute". Science History Institute. يونيو 2016. Retrieved 2 يونيو 2022.
^ Perrin, Jean (1909). "Mouvement brownien et réalité moléculaire" [Brownian movement and molecular reality]. Annales de Chimie et de Physique. 8th series (in الفرنسية). 18: 1–114. Extract in English, translation by Frederick Soddy.
^ Loschmidt, J. (1865). "Zur Grösse der Luftmoleküle" [On the size of air molecules]. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch-Naturwissenschaftliche Classe. Wien (in الألمانية). 52 (2): 395–413. English translation.
^ ^أ ^ب ^ت Bureau International des Poids et Mesures (1971): 14th Conference Générale des Poids et Mesures Archived 2020-09-23 at the Wayback Machine Available at the BIPM website.
^ H. P. Lehmann, X. Fuentes-Arderiu, and L. F. Bertello (1996): "Glossary of terms in quantities and units in Clinical Chemistry (IUPAC-IFCC Recommendations 1996)"; p. 963, item "Avogadro constant". Pure and Applied Chemistry, vol. 68, iss. 4, pp. 957–1000. DOI:10.1351/pac199668040957
^ Virgo, S.E. (1933). "Loschmidt's Number". Science Progress. 27: 634–649. Archived from the original on 4 أبريل 2005.
^ Oseen, C.W. (December 10, 1926). Presentation Speech for the 1926 Nobel Prize in Physics.
^ (1974): Introduction to the constants for nonexperts, 1900–1920 From the Encyclopaedia Britannica, 15th ed.; reproduced by NIST. Accessed on 2019-07-03.
^ Kotz, John C.; Treichel, Paul M.; Townsend, John R. (2008). Chemistry and Chemical Reactivity (7th ed.). Brooks/Cole. ISBN 978-0-495-38703-9. Archived from the original on 16 أكتوبر 2008.
^ International Bureau for Weights and Measures (2017): Proceedings of the 106th meeting of the International Committee for Weights and Measures (CIPM), 16-17 and 20 October 2017, p. 23. Available at the BIPM website Archived 2021-02-21 at the Wayback Machine.
^ Pavese, Franco (يناير 2018). "A possible draft of the CGPM Resolution for the revised SI, compared with the CCU last draft of the 9th SI Brochure". Measurement. 114: 478–483. Bibcode:2018Meas..114..478P. doi:10.1016/j.measurement.2017.08.020. ISSN 0263-2241.
^ "Unified atomic mass unit". The IUPAC Compendium of Chemical Terminology. 2014. doi:10.1351/goldbook.U06554.
^ Bureau International des Poids et Mesures (2019): The International System of Units (SI), 9th edition, English version, p. 134. Available at the BIPM website.
^ "CODATA Value: atomic mass constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. يونيو 2011. Retrieved 23 يونيو 2011. {{cite web}}: External link in |work= (help)

خطأ استشهاد: الوسم <ref> ذو الاسم "feynman" المُعرّف في <references> غير مستخدم في النص السابق.
خطأ استشهاد: الوسم <ref> ذو الاسم "born" المُعرّف في <references> غير مستخدم في النص السابق.

خطأ استشهاد: الوسم <ref> ذو الاسم "ciaaw" المُعرّف في <references> غير مستخدم في النص السابق.

وصلات خارجية

1996 definition of the Avogadro constant from the IUPAC Compendium of Chemical Terminology ("Gold Book")
Some Notes on Avogadro's Number, 6.022×10²³ (historical notes)
An Exact Value for Avogadro's Number – American Scientist
Avogadro and molar Planck constants for the redefinition of the kilogram
Murrell, John N. (2001). "Avogadro and His Constant". Helvetica Chimica Acta. 84 (6): 1314–1327. doi:10.1002/1522-2675(20010613)84:6<1314::AID-HLCA1314>3.0.CO;2-Q.
Scanned version of "Two hypothesis of Avogadro", 1811 Avogadro's article, on BibNum

?

[okun-1] Okun, Lev B.; Lee, A. G. (1985). Particle Physics: The Quest for the Substance of Substance. OPA Ltd. p. 86. ISBN 978-3-7186-0228-5.

[bipm8th-2] أ ^ب قالب:SIbrochure8th

[NIST2019-3] أ ^ب ^ت ^ث ^ج David B. Newell and Eite Tiesinga (2019): The International System of Units (SI). NIST Special Publication 330, National Institute of Standards and Technology. DOI:10.6028/nist.sp.330-2019 قالب:S2cid

[pauling-4] Linus Pauling (1970), General Chemistry, p. 96. Dover Edition, reprinted by Courier in 2014; 992 pages. ISBN 978-0486134659

[mcgraw-5] Marvin Yelles (1971): McGraw-Hill Encyclopedia of Science and Technology, Vol. 9, 3rd ed.; 707 pages. ISBN 978-0070797987

[avog1811-6] Avogadro, Amedeo (1811). "Essai d'une maniere de determiner les masses relatives des molecules elementaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons". Journal de Physique. 73: 58–76. English translation.

[7] "Stanislao Cannizzaro | Science History Institute". Science History Institute. يونيو 2016. Retrieved 2 يونيو 2022.

[perrin1909-8] Perrin, Jean (1909). "Mouvement brownien et réalité moléculaire" [Brownian movement and molecular reality]. Annales de Chimie et de Physique. 8th series (in الفرنسية). 18: 1–114. Extract in English, translation by Frederick Soddy.

[losch1865-9] Loschmidt, J. (1865). "Zur Grösse der Luftmoleküle" [On the size of air molecules]. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch-Naturwissenschaftliche Classe. Wien (in الألمانية). 52 (2): 395–413. English translation.

[bipm1971-10] أ ^ب ^ت Bureau International des Poids et Mesures (1971): 14th Conference Générale des Poids et Mesures Archived 2020-09-23 at the Wayback Machine Available at the BIPM website.

[iupac1996-11] H. P. Lehmann, X. Fuentes-Arderiu, and L. F. Bertello (1996): "Glossary of terms in quantities and units in Clinical Chemistry (IUPAC-IFCC Recommendations 1996)"; p. 963, item "Avogadro constant". Pure and Applied Chemistry, vol. 68, iss. 4, pp. 957–1000. DOI:10.1351/pac199668040957

[virgo1933-12] Virgo, S.E. (1933). "Loschmidt's Number". Science Progress. 27: 634–649. Archived from the original on 4 أبريل 2005.

[oseen1926-13] Oseen, C.W. (December 10, 1926). Presentation Speech for the 1926 Nobel Prize in Physics.

[ebrit1974-14] (1974): Introduction to the constants for nonexperts, 1900–1920 From the Encyclopaedia Britannica, 15th ed.; reproduced by NIST. Accessed on 2019-07-03.

[kotz2008-15] Kotz, John C.; Treichel, Paul M.; Townsend, John R. (2008). Chemistry and Chemical Reactivity (7th ed.). Brooks/Cole. ISBN 978-0-495-38703-9. Archived from the original on 16 أكتوبر 2008.

[cipm106-16] International Bureau for Weights and Measures (2017): Proceedings of the 106th meeting of the International Committee for Weights and Measures (CIPM), 16-17 and 20 October 2017, p. 23. Available at the BIPM website Archived 2021-02-21 at the Wayback Machine.

[pave2018-17] Pavese, Franco (يناير 2018). "A possible draft of the CGPM Resolution for the revised SI, compared with the CCU last draft of the 9th SI Brochure". Measurement. 114: 478–483. Bibcode:2018Meas..114..478P. doi:10.1016/j.measurement.2017.08.020. ISSN 0263-2241.

[IUPAC-18] "Unified atomic mass unit". The IUPAC Compendium of Chemical Terminology. 2014. doi:10.1351/goldbook.U06554.

[bipm9th-19] Bureau International des Poids et Mesures (2019): The International System of Units (SI), 9th edition, English version, p. 134. Available at the BIPM website.

[physconst-mu-20] "CODATA Value: atomic mass constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. يونيو 2011. Retrieved 23 يونيو 2011. {{cite web}}: External link in |work= (help)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]