جوار (رياضيات)

المجموعة V في المستوي هي جوار للنقطة p إذا وجد قرص صغير يحيط بالنقطة p ومحتوى بكامله في V.

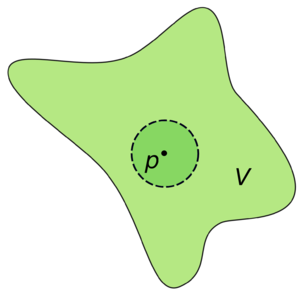
في الطوبولوجيا، الجوار Neighbourhood هو واحد من أبسط مفاهيم الفضاء الطوبولوجي. حيث يعرف جوار نقطة على أنه المجموعة التي تحتوي النقطة بحيث أن النقطة تكون محاطة دون الخروج خارج المجموعة.

مفهوم الجوار يقارب جداً مفهوما المجموعة المفتوحة والداخل.

 تعريفات

 جوار نقطة

If ${\displaystyle{\displaystyle X}}$ is a topological space and ${\displaystyle{\displaystyle p}}$ is a point in ${\displaystyle{\displaystyle X,}}$ then a neighbourhood of ${\displaystyle{\displaystyle p}}$ is a subset ${\displaystyle{\displaystyle V}}$ of ${\displaystyle{\displaystyle X}}$ that includes an open set ${\displaystyle{\displaystyle U}}$ containing ${\displaystyle{\displaystyle p}}$,

$$p\in U\subseteq V\subseteq X.$$

This is also equivalent to the point ${\displaystyle{\displaystyle p\in X}}$ belonging to the topological interior of ${\displaystyle{\displaystyle V}}$ in ${\displaystyle{\displaystyle X.}}$

The neighbourhood ${\displaystyle{\displaystyle V}}$ need not be an open subset ${\displaystyle{\displaystyle X,}}$ but when ${\displaystyle{\displaystyle V}}$ is open in ${\displaystyle{\displaystyle X}}$ then it is called an open neighbourhood. Some authors have been known to require neighbourhoods to be open, so it is important to note conventions.

المستطيل المغلق لا يعتبر جواراً لأي من زواياه أو حدوده.

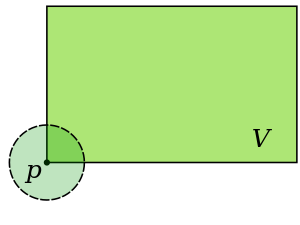
A set that is a neighbourhood of each of its points is open since it can be expressed as the union of open sets containing each of its points. A rectangle, as illustrated in the figure, is not a neighbourhood of all its points; points on the edges or corners of the rectangle are not contained in any open set that is contained within the rectangle.

The collection of all neighbourhoods of a point is called the neighbourhood system at the point.

 جوار فئة

If ${\displaystyle{\displaystyle S}}$ is a subset of a topological space ${\displaystyle{\displaystyle X}}$, then a neighbourhood of ${\displaystyle{\displaystyle S}}$ is a set ${\displaystyle{\displaystyle V}}$ that includes an open set ${\displaystyle{\displaystyle U}}$ containing ${\displaystyle{\displaystyle S}}$,

$$S\subseteq U\subseteq V\subseteq X.$$

It follows that a set

${\displaystyle{\displaystyle V}}$

is a neighbourhood of

${\displaystyle{\displaystyle S}}$

if and only if it is a neighbourhood of all the points in

${\displaystyle{\displaystyle S.}}$

Furthermore,

${\displaystyle{\displaystyle V}}$

is a neighbourhood of

${\displaystyle{\displaystyle S}}$

if and only if

${\displaystyle{\displaystyle S}}$

is a subset of the interior of

${\displaystyle{\displaystyle V.}}$

A neighbourhood of

${\displaystyle{\displaystyle S}}$

that is also an open subset of

${\displaystyle{\displaystyle X}}$

is called an open neighbourhood of

${\displaystyle{\displaystyle S.}}$

The neighbourhood of a point is just a special case of this definition.

 في فضاء قياسي

الفئة ${\displaystyle{\displaystyle S}}$ في المستوى وجوار منتظم ${\displaystyle{\displaystyle V}}$ في ${\displaystyle{\displaystyle S.}}$

الجوار إپسيلون للعدد ${\displaystyle{\displaystyle a}}$ على خط أعداد حقيقية.

In a metric space ${\displaystyle{\displaystyle M=(X,d),}}$ a set ${\displaystyle{\displaystyle V}}$ is a neighbourhood of a point ${\displaystyle{\displaystyle p}}$ if there exists an open ball with center ${\displaystyle{\displaystyle p}}$ and radius ${\displaystyle{\displaystyle r>0,}}$ such that

$$B_{r}(p)=B(p;r)=\{x\in X:d(x,p)<r\}$$

is contained in

${\displaystyle{\displaystyle V.}}$

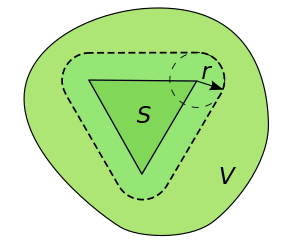
${\displaystyle{\displaystyle V}}$ is called uniform neighbourhood of a set ${\displaystyle{\displaystyle S}}$ if there exists a positive number ${\displaystyle{\displaystyle r}}$ such that for all elements ${\displaystyle{\displaystyle p}}$ of ${\displaystyle{\displaystyle S,}}$

$$B_{r}(p)=\{x\in X:d(x,p)<r\}$$

is contained in

${\displaystyle{\displaystyle V.}}$

For ${\displaystyle{\displaystyle r>0,}}$ the ${\displaystyle{\displaystyle r}}$-neighbourhood ${\displaystyle{\displaystyle S_{r}}}$ of a set ${\displaystyle{\displaystyle S}}$ is the set of all points in ${\displaystyle{\displaystyle X}}$ that are at distance less than ${\displaystyle{\displaystyle r}}$ from ${\displaystyle{\displaystyle S}}$ (or equivalently, ${\displaystyle{\displaystyle S_{r}}}$ is the union of all the open balls of radius ${\displaystyle{\displaystyle r}}$ that are centered at a point in ${\displaystyle{\displaystyle S}}$):

$$S_{r}=\bigcup\limits_{p\in{}S}B_{r}(p).$$

It directly follows that an ${\displaystyle{\displaystyle r}}$-neighbourhood is a uniform neighbourhood, and that a set is a uniform neighbourhood if and only if it contains an ${\displaystyle{\displaystyle r}}$-neighbourhood for some value of ${\displaystyle{\displaystyle r.}}$

 مراجع (بالإنگليزية)

• Kelley, John L. (1975). General topology. New York: Springer-Verlag. ISBN 0387901256.

• Bredon, Glen E. (1993). Topology and geometry. New York: Springer-Verlag. ISBN 0387979263.

• Kaplansky, Irving (2001). Set Theory and Metric Spaces. American Mathematical Society. ISBN 0821826948.