طاقة موجية

الطاقة المتجدّدة
طاقة حيوية كتلة حيوية طاقة حرارية أرضية طاقة مائية طاقة شمسية طاقة المد والجزر طاقة موجية طاقة الرياح

الطاقة الموجية إنگليزية: Wave power هي نقل الطاقة من أمواج المحيط السطحية، و تسخيرها في اشغال ميكانيكية مفيدة مثل توليد الكهرباء، تحلية المياه أو ضخ المياة إلى المخازن المائية.

و تعتبر أحد أنواع الطاقة المتجددة. و هي تختلف كليا عن طاقة المد والجزر. و لا زالت تقنية الطاقة الموجية حاليا غير موظفة تجاريا مع العلم بوجود بوادر إستعمالها منذ عام 1890 على الأقل. و توجد أول مزرعة موجية في العالم في البرتغال، و تحتوي على ثلاثة محولات بقوة 750 كيلو واط للمحول الواحد.

 المفاهيم الفيزيائية

المقالة الرئيسية: Airy wave theory

Like most fluid motion, the interaction between ocean waves and energy converters is a high-order nonlinear phenomenon. It is described using the incompressible Navier-Stokes equations

$${\displaystyle{\begin{aligned} \displaystyle{\frac{\partial{\vec{u}}}{\partial t}}+({\vec{u}}\cdot{\vec{\nabla}}){\vec{u}}&\displaystyle=\nu\Delta{\vec{u}}+{\frac{{\vec{F_{\text{ext}}}}-{\vec{\nabla}}p}{\rho}}\\ \displaystyle{\vec{\nabla}}\cdot{\vec{u}}&\displaystyle=0\end{aligned}}}$$

where

${\textstyle{\vec{u}}(t,x,y,z)}$

is the fluid velocity,

${\textstyle p}$

is the pressure,

${\textstyle\rho}$

the density,

${\textstyle\nu}$

the viscosity, and

${\textstyle{\vec{F_{\text{ext}}}}}$

the net external force on each fluid particle (typically gravity). Under typical conditions, however, the movement of waves is described by Airy wave theory, which posits that

• fluid motion is roughly irrotational,
• pressure is approximately constant at the water surface, and
• the seabed depth is approximately constant.

In situations relevant for energy harvesting from ocean waves these assumptions are usually valid.

 Airy equations

The first condition implies that the motion can be described by a velocity potential ${\textstyle\phi(t,x,y,z)}$:

$${\displaystyle{{\vec{\nabla}}\times{\vec{u}}={\vec{0}}}\Leftrightarrow{{\vec{u}}={\vec{\nabla}}\phi}{\text{,}}}$$

which must satisfy the Laplace equation,

$${\displaystyle\nabla^{2}\phi=0{\text{.}}}$$

In an ideal flow, the viscosity is negligible and the only external force acting on the fluid is the earth gravity

${\displaystyle{\displaystyle{\vec{F_{\text{ext}}}}=(0,0,-\rho g)}}$

. In those circumstances, the Navier-Stokes equations reduces to

$${\displaystyle{\partial{\vec{\nabla}}\phi\over\partial t}+{1\over 2}{\vec{\nabla}}{\bigl{(}}{\vec{\nabla}}\phi{\bigr{)}}^{2}=-{1\over\rho}\cdot{\vec{\nabla}}p+{1\over\rho}{\vec{\nabla}}{\bigl{(}}\rho gz{\bigr{)}},}$$

which integrates (spatially) to the Bernoulli conservation law:

$${\displaystyle{\partial\phi\over\partial t}+{1\over 2}{\bigl{(}}{\vec{\nabla}}\phi{\bigr{)}}^{2}+{1\over\rho}p+gz=({\text{const}}){\text{.}}}$$

 Linear potential flow theory

Motion of a particle in an ocean wave.
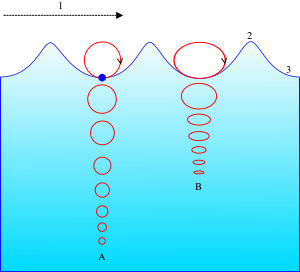
A = At deep water. The circular motion magnitude of fluid particles decreases exponentially with increasing depth below the surface.
B = At shallow water (ocean floor is now at B). The elliptical movement of a fluid particle flattens with decreasing depth.
1 = Propagation direction.
2 = Wave crest.
3 = Wave trough.

When considering small amplitude waves and motions, the quadratic term ${\textstyle\left({\vec{\nabla}}\phi\right)^{2}}$ can be neglected, giving the linear Bernoulli equation,

$${\displaystyle{\partial\phi\over\partial t}+{1\over\rho}p+gz=({\text{const}}){\text{.}}}$$

and third Airy assumptions then imply

$${\displaystyle{\begin{aligned} &\displaystyle{\partial^{2}\phi\over\partial t^{2}}+g{\partial\phi\over\partial z}=0\quad\quad\quad({\text{surface}})\\ &\displaystyle{\partial\phi\over\partial z}=0{\phantom{{\partial^{2}\phi\over\partial t^{2}}+{}}}\,\,\quad\quad\quad({\text{seabed}})\end{aligned}}}$$

These constraints entirely determine sinusoidal wave solutions of the form

$${\displaystyle\phi=A(z)\sin{\!(kx-\omega t)}{\text{,}}}$$

where

${\displaystyle{\displaystyle k}}$

determines the wavenumber of the solution and

${\displaystyle{\displaystyle A(z)}}$

and

${\displaystyle{\displaystyle\omega}}$

are determined by the boundary constraints (and

${\displaystyle{\displaystyle k}}$

). Specifically,

$${\displaystyle{\begin{aligned} &\displaystyle A(z)={gH\over 2\omega}{\cosh(k(z+h))\over\cosh(kh)}\\ &\displaystyle\omega=gk\tanh(kh){\text{.}}\end{aligned}}}$$

The surface elevation

${\displaystyle{\displaystyle\eta}}$

can then be simply derived as

$${\displaystyle\eta=-{1\over g}{\partial\phi\over\partial t}={H\over 2}\cos(kx-\omega t){\text{:}}}$$

a plane wave progressing along the x-axis direction.

 Consequences

Oscillatory motion is highest at the surface and diminishes exponentially with depth. However, for standing waves (clapotis) near a reflecting coast, wave energy is also present as pressure oscillations at great depth, producing microseisms. Pressure fluctuations at greater depth are too small to be interesting for wave power conversion.

The behavior of Airy waves offers two interesting regimes: water deeper than half the wavelength, as is common in the sea and ocean, and shallow water, with wavelengths larger than about twenty times the water depth. Deep waves are dispersionful: Waves of long wavelengths propagate faster and tend to outpace those with shorter wavelengths. Deep-water group velocity is half the phase velocity. Shallow water waves are dispersionless: group velocity is equal to phase velocity, and wavetrains propagate undisturbed.

The following table summarizes the behavior of waves in the various regimes:

Airy gravity waves on the surface of deep water, shallow water, or intermediate depth

quantity	symbol	units	deep water (h > 1⁄2 λ)	shallow water (h < 0.05 λ)	intermediate depth (all λ and h)
phase velocity	${\displaystyle{\displaystyle c_{p}={\frac{\lambda}{T}}={\frac{\omega}{k}}}}$	m / s	${\displaystyle{\displaystyle{\frac{g}{2\pi}}T}}$	${\displaystyle{\displaystyle{\sqrt{gh}}}}$	${\displaystyle{\displaystyle{\sqrt{{\frac{g\lambda}{2\pi}}\tanh\left({\frac{2\pi h}{\lambda}}\right)}}}}$
group velocity	${\displaystyle{\displaystyle c_{g}=c_{p}^{2}{\frac{\partial\left(\lambda/c_{p}\right)}{\partial\lambda}}={\frac{\partial\omega}{\partial k}}}}$	m / s	${\displaystyle{\displaystyle{\frac{g}{4\pi}}T}}$	${\displaystyle{\displaystyle{\sqrt{gh}}}}$	${\displaystyle{\displaystyle{\frac{1}{2}}c_{p}\left(1+{\frac{4\pi h}{\lambda}}{\frac{1}{\sinh\left({\frac{4\pi h}{\lambda}}\right)}}\right)}}$
ratio	${\displaystyle{\displaystyle{\frac{c_{g}}{c_{p}}}}}$	–	${\displaystyle{\displaystyle{\frac{1}{2}}}}$	${\displaystyle{\displaystyle 1}}$	${\displaystyle{\displaystyle{\frac{1}{2}}\left(1+{\frac{4\pi h}{\lambda}}{\frac{1}{\sinh\left({\frac{4\pi h}{\lambda}}\right)}}\right)}}$
wavelength	${\displaystyle{\displaystyle\lambda}}$	m	${\displaystyle{\displaystyle{\frac{g}{2\pi}}T^{2}}}$	${\displaystyle{\displaystyle T{\sqrt{gh}}}}$	for given period T, the solution of:   ${\displaystyle{\displaystyle\left({\frac{2\pi}{T}}\right)^{2}={\frac{2\pi g}{\lambda}}\tanh\left({\frac{2\pi h}{\lambda}}\right)}}$
general
wave energy density	${\displaystyle{\displaystyle E}}$	J / m2	${\displaystyle{\displaystyle{\frac{1}{16}}\rho gH_{m0}^{2}}}$
wave energy flux	${\displaystyle{\displaystyle P}}$	W / m	${\displaystyle{\displaystyle E\;c_{g}}}$
angular frequency	${\displaystyle{\displaystyle\omega}}$	rad / s	${\displaystyle{\displaystyle{\frac{2\pi}{T}}}}$
wavenumber	${\displaystyle{\displaystyle k}}$	rad / m	${\displaystyle{\displaystyle{\frac{2\pi}{\lambda}}}}$

 Wave power formula

Photograph of the elliptical trajectories of water particles under a – progressive and periodic – surface gravity wave in a wave flume. The wave conditions are: mean water depth d = 2.50 ft (0.76 m), wave height H = 0.339 ft (0.103 m), wavelength λ = 6.42 ft (1.96 m), period T = 1.12 s.

In deep water where the water depth is larger than half the wavelength, the wave energy flux is

${\displaystyle{\displaystyle P={\frac{\rho g^{2}}{64\pi}}H_{m0}^{2}T_{e}\approx\left(0.5{\frac{\text{kW}}{{\text{m}}^{3}\cdot{\text{s}}}}\right)H_{m0}^{2}\;T_{e},}}$

with P the wave energy flux per unit of wave-crest length, H_m0 the significant wave height, T_e the wave energy period, ρ the water density and g the acceleration by gravity. The above formula states that wave power is proportional to the wave energy period and to the square of the wave height. When the significant wave height is given in metres, and the wave period in seconds, the result is the wave power in kilowatts (kW) per metre of wavefront length.

For example, consider moderate ocean swells, in deep water, a few km off a coastline, with a wave height of 3 m and a wave energy period of 8 s. Solving for power produces

${\displaystyle{\displaystyle P\approx 0.5{\frac{\text{kW}}{{\text{m}}^{3}\cdot{\text{s}}}}(3\cdot{\text{m}})^{2}(8\cdot{\text{s}})\approx 36{\frac{\text{kW}}{\text{m}}},}}$

or 36 kilowatts of power potential per meter of wave crest.

In major storms, the largest offshore sea states have significant wave height of about 15 meters and energy period of about 15 seconds. According to the above formula, such waves carry about 1.7 MW of power across each meter of wavefront.

An effective wave power device captures a significant portion of the wave energy flux. As a result, wave heights diminish in the region behind the device.

 Energy and energy flux

In a sea state, the mean energy density per unit area of gravity waves on the water surface is proportional to the wave height squared, according to linear wave theory:

${\displaystyle{\displaystyle E={\frac{1}{16}}\rho gH_{m0}^{2},}}$

where E is the mean wave energy density per unit horizontal area (J/m²), the sum of kinetic and potential energy density per unit horizontal area. The potential energy density is equal to the kinetic energy, both contributing half to the wave energy density E, as can be expected from the equipartition theorem.

The waves propagate on the surface, where crests travel with the phase velocity while the energy is transported horizontally with the group velocity. The mean transport rate of the wave energy through a vertical plane of unit width, parallel to a wave crest, is the energy flux (or wave power, not to be confused with the output produced by a device), and is equal to:

${\displaystyle{\displaystyle P=E\,c_{g},}}$ with c_g the group velocity (m/s).

Due to the dispersion relation for waves under gravity, the group velocity depends on the wavelength λ, or equivalently, on the wave period T.

Wave height is determined by wind speed, the length of time the wind has been blowing, fetch (the distance over which the wind excites the waves) and by the bathymetry (which can focus or disperse the energy of the waves). A given wind speed has a matching practical limit over which time or distance do not increase wave size. At this limit the waves are said to be "fully developed". In general, larger waves are more powerful but wave power is also determined by wavelength, water density, water depth and acceleration of gravity.

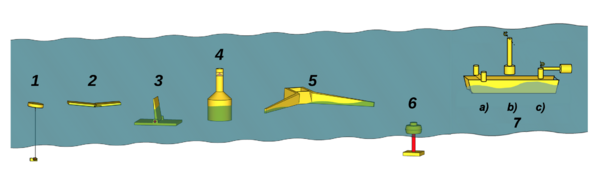
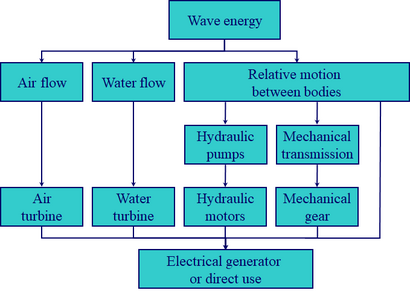
 محولات الطاقة الموجية

Generic wave energy concepts: 1. Point absorber, 2. Attenuator, 3. Oscillating wave surge converter, 4. Oscillating water column, 5. Overtopping device, 6. Submerged pressure differential, 7. Floating in-air converters.

Wave energy converters (WECs) are generally categorized by the method, by location and by the power take-off system. Locations are shoreline, nearshore and offshore. Types of power take-off include: hydraulic ram, elastomeric hose pump, pump-to-shore, hydroelectric turbine, air turbine, and linear electrical generator.

Different conversion routes from wave energy to useful energy in terms or electricity or direct use.

The four most common approaches are:

• point absorber buoys
• surface attenuators
• oscillating water columns
• overtopping devices

 Point absorber buoy

This device floats on the surface, held in place by cables connected to the seabed. The point-absorber has a device width much smaller than the incoming wavelength λ. Energy is absorbed by radiating a wave with destructive interference to the incoming waves. Buoys use the swells' rise and fall to generate electricity directly via linear generators, generators driven by mechanical linear-to-rotary converters, or hydraulic pumps. Energy extracted from waves may affect the shoreline, implying that sites should remain well offshore.

One point absorber design tested at commercial scale by CorPower features a negative spring that improves performance and protects the buoy in very large waves. It also has an internal pneumatic cylinder that keeps the buoy at a fixed distance from the seabed regardless of the state of the tide. Under normal operating conditions, the buoy bobs up and down at double the wave amplitude by adjusting the phase of its movements. It rises with a slight delay from the wave, which allows it to extract more energy. The firm claimed a 300% increase (600 kW) in power generation compared to a buoy without phase adjustments in tests completed in 2024.

 Surface attenuator

These devices use multiple floating segments connected to one another. They are oriented perpendicular to incoming waves. A flexing motion is created by swells, and that motion drives hydraulic pumps to generate electricity. The Pelamis Wave Energy Converter is one of the more well-known attenuator concepts, although this is no longer being developed.

 Oscillating wave surge converter

These devices typically have one end fixed to a structure or the seabed while the other end is free to move. Energy is collected from the relative motion of the body compared to the fixed point. Converters often come in the form of floats, flaps, or membranes. Some designs incorporate parabolic reflectors to focus energy at the point of capture. These systems capture energy from the rise and fall of waves.

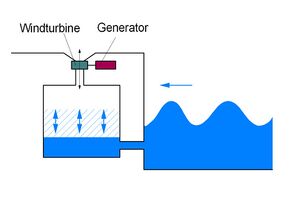
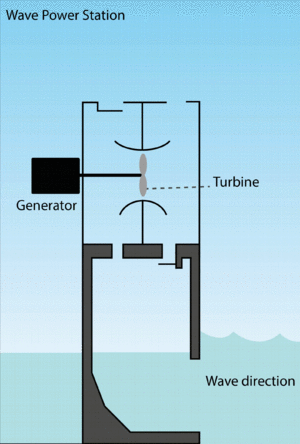
 Oscillating water column

Oscillating water column devices can be located onshore or offshore. Swells compress air in an internal chamber, forcing air through a turbine to create electricity. Significant noise is produced as air flows through the turbines, potentially affecting nearby birds and marine organisms. Marine life could possibly become trapped or entangled within the air chamber. It draws energy from the entire water column.

 Overtopping device

Overtopping devices are long structures that use wave velocity to fill a reservoir to a greater water level than the surrounding ocean. The potential energy in the reservoir height is captured with low-head turbines. Devices can be on- or offshore.

 Submerged pressure differential

Submerged pressure differential based converters use flexible (typically reinforced rubber) membranes to extract wave energy. These converters use the difference in pressure at different locations below a wave to produce a pressure difference within a closed power take-off hydraulic system. This pressure difference is usually used to produce flow, which drives a turbine and electrical generator. Submerged pressure differential converters typically use flexible membranes as the working surface between the water and the power take-off. Membranes are pliant and low mass, which can strengthen coupling with the wave's energy. Their pliancy allows large changes in the geometry of the working surface, which can be used to tune the converter for specific wave conditions and to protect it from excessive loads in extreme conditions.

A submerged converter may be positioned either on the seafloor or in midwater. In both cases, the converter is protected from water impact loads which can occur at the free surface. Wave loads also diminish in non-linear proportion to the distance below the free surface. This means that by optimizing depth, protection from extreme loads and access to wave energy can be balanced.

 Floating in-air converters

Wave Power Station using a pneumatic Chamber

Simplified design of Wave Power Station

Floating in-air converters potentially offer increased reliability because the device is located above the water, which also eases inspection and maintenance. Examples of different concepts of floating in-air converters include:

• roll damping energy extraction systems with turbines in compartments containing sloshing water
• horizontal axis pendulum systems
• vertical axis pendulum systems

 Submerged wave energy converters

In early 2024, a fully submerged wave energy converter using point absorber-type wave energy technology was approved in Spain. The converter includes a buoy that is moored to the bottom and situated below the surface, out of sight of people and away from storm waves.

 وصلات خارجية

• Kate Galbraith (September 22, 2008). "Power From the Restless Sea Stirs the Imagination". New York Times. Retrieved 2008-10-09.
• "Wave Power: The Coming Wave" from the Economist, June 5, 2008
• "Is wave power commercially viable?"
• "The untimely death of Salter's Duck"
• "Ocean Power Fights Current Thinking"
• "Wave energy in New Zealand"
• "How it works: Wave power station"
• Waves power future from the Corvallis Gazette Times, February 5, 2005
• EU Wavetrain project — A series of full-text, on-line scientific publications on physical concepts.
• Make the Waves Operate a Motor-Boat Bilge-Pump, Popular Science monthly, February 1919, Unnumbered page, Scanned by Google Books: http://books.google.com/books?id=7igDAAAAMBAJ&pg=PT24