لا مركزية (رياضيات)

اللامركزية في الرياضيات (Eccentricity) مصطلح يتعلق بالمقاطع المخروطية وهو مقياس لمدى ابتعاد هذا المقطع عن كونه دائريا.

 المخروطيات

المخروطيات conic أو المقطع المخروطي conic section هي كل منحني ينتج عن قطع المخروط بمستوي في اتجاه ما .

 تعريف مخروطي بالبؤرة و الدليل و التباعد المركزي

في مستوى, عندنا مستقيم D (الدليل) و نقطة F (البؤرة) و e عدد حقيقي موجب (التباعد المركزي).

مجموعة نقط المستوى M, التي تحقق الشرط: MF=eMm. مع :Mm المسافة بين M و D, تسمى مخروطي ذا البؤرة F و الدليل D و التباعد المركزي e.

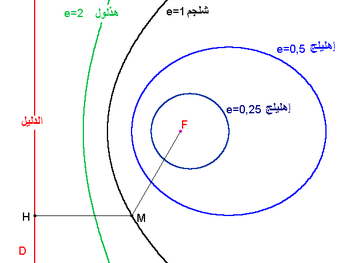
 تصنيف مخروطي حسب قيم e

• إذا كان e=1, فالمخروطي يسمى: قطعا مكافيء (شلجما) parapola .
• إذا كان 0<e و e<1, فالمخروطي يسمى: إهليلجا.
• إذا كان e=0, فالمخروطي يسمى: دائرة.
• إذا كان 1<e, فالمخروطي يسمى: قطعا زائدا (هذلولا) hyperbola .

 داخل و خارج مخروطي

• M نقطة داخل المخروطي: MF-eMm<0.
• M نقطة خارج المخروطي: MF-eMm>0.

البؤرة توجد داخل المخروطي, و الدليل يوجد خارجه.

العمودي على D المار من F, محور تماثل المخروطي و يسمى المحور البؤري.

 رؤوس مخروطي

1. إذا كان e=1 فالمحور البؤري (fK) يقطع المخروطي في نقطة واحدة هي منتصف FK, و تسمى رأس المخروطي.
2. إذا كان e#1 فالمحور البؤري (fK) يقطع المخروطي في نقطتين مختلفتين هما رأسي المخروطي.

 دراسة الإهليلج

 خصائص إهليلج

للإهليلج محور كبير, و محور صغير. المحوران متعامدان و يتقاطعان في نقطة تسمى مركز الإهليلج.

 المعادلة المختصرة

• 2a طول المحور الكبير.
• 2b طول المحور الصغير.

معادلة الإهليلج هي: ${\displaystyle{\displaystyle\qquad{\frac{x^{2}}{a^{2}}}+{\frac{y^{2}}{b^{2}}}=1}}$

 التعريف البؤرتاني للإهليلج

الإهليلج ذو البؤرتين F و F' الذي محوره الكبير هو 2a هو مجموعة النقط M التي تحقق: MF+MF'=2a.

 المعادلة البارامترية للإهليلج

${\displaystyle{\displaystyle\qquad\left\{{\begin{matrix}{\begin{matrix}x&=&a\cos t\\ y&=&b\sin t\end{matrix}}\\ t\in[0,2\pi[\end{matrix}}\right.}}$