مبرهنة كارنو

${\displaystyle{\displaystyle{\begin{aligned} &\displaystyle{}\qquad DG+DH+DF\\ &\displaystyle{}=|DG|+|DH|-|DF|\\ &\displaystyle{}=R+r\end{aligned}}}}$

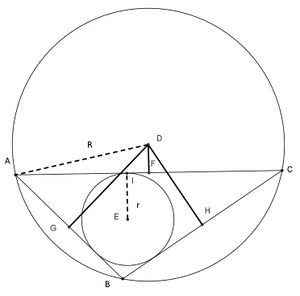
في الهندسة الإقليدية، تنص مبرهنة كارنو التي سميت على اسم لازار كارنو (1753 - 1823) مايلي: هب أن ABC مثلث ما، فإن مجموع المسافات من الدائرة المحيطة D إلى أضلاع المثلث ABC تحقق العلاقة:

DF + DG + DH = R + r,

حيث r نصف القطر الدائرة المحاطة، R نصف قطر الدائرة المحيطة. وتأخذ إشارة المسافة على أنها سالبة إذا كانت القطعة المستقيمة DX (X = F, G, H) تقع بكاملها خارج المثلث. حيث في الصورة الموضحة القطعة المستقيمة DF تكون ذات طول سالب، والقطعتين المستقيمتين DGو DH موجبتان.

تستخدم مبرهنة كارنو في برهان مبرهنة يابانية في مضلع دائري.

 وصلات خارجية

• Eric W. Weisstein, مبرهنة كارنوت at MathWorld.