مسألة NP كاملة

مسألة NP كاملة
قابلية الإرضاء 3SAT NAE OIT
تلوين مخطط تلوين مخطط بثلاثة ألوان تلوين مخطط مستو بثلاثة ألوان
زمرة كبرى
مسار هاملتونياني
عدل

في الرياضيات صنف التعقيد، تُعرف المسائل NP الكاملة، بأنها كل ما يحقق الشرطين الآتيين:

• كل مسألة من صنف NP، تختصر لمسألة واحدة A.
• المسألة A من صنف NP.

لتحديد وجودية المسائل NP الكاملة، قام كوك و كيفين باستعمال آلة تورينغ للبرهنة على وجود مسألة NP الكاملة، و هي صيغة قيم ثنائية مكونة من عطف عدة صيغ كل صيغة هي مجموعة فصل عدة متغيرات ثنائية أي لها 1 أو 0 كقيمة.

 مبرهنة كوك و ليفين

نص المبرهنة هو: SAT مشكل حدودي غير محدد كامل (NP-compet).

تنسب في الأغلب لكوك، حيث أن ليفين وجد نفس النتائج دون أن يكون على علم بنتائج كوك، ففي ذلك الوقت لم تكن هناك وسائل اتصال متطورة (ما بين 1971 و 1974).

 مفهوم الإختصار

نقول أن ${\displaystyle{\displaystyle L_{1}}}$ يتم اختصاره إلى ${\displaystyle{\displaystyle L_{2}}}$ في وقت حدودي، في حالة وجود دالة قابلة للحساب في وقت حدودي، ${\displaystyle{\displaystyle f:\left\{0,1\right\}^{*}\rightarrow\left\{0,1\right\}^{*}}}$ يحيث لكل ${\displaystyle{\displaystyle x\in\left\{0,1\right\}^{*}}}$, ${\displaystyle{\displaystyle x\in L_{1}}}$ إذا و فقط إذا كان ${\displaystyle{\displaystyle f(x)\in L_{2}}}$. نسمي الدالة ${\displaystyle{\displaystyle f\!}}$ دالة الإختصار, و خوارزمية حدودية التي تحسب ${\displaystyle{\displaystyle f\!}}$ يسمى خوارزمية الإختصار.

 البرهنة

نقدم هنا برهنة تقريبية.

A مسألة من صنف NP. هذه المسألة مقبولة من آلة تورينغ M غير محددة. بالنسبة لكل مداخلة w ل M، توجد صيغة ${\displaystyle{\displaystyle\varphi_{w}}}$ ذات بعد حدودي بالنسبة لبعد w و التي تكون كافية إذا و فقط إذا كانت w مقبولة من M.

نرمز ل ${\displaystyle{\displaystyle n=|w|}}$ بعد w. بما أن الآلة M تعمل في وقت حدودي، يوجد عدد طبيعي ثابت k حيث كل عملية حسابية على w تكون على الأكثر بطول ${\displaystyle{\displaystyle n^{k}}}$. نضيف سلسلة انتظار مغلقة، و نفترض أن طول العمليات هو بالضبط ${\displaystyle{\displaystyle n^{k}}}$. آلة تورينغ تستعمل ${\displaystyle{\displaystyle n^{k}}}$ خلية. الإعدادات الخاصة بحساب مقبول يكون أيضا بطول ${\displaystyle{\displaystyle n^{k}}}$. عند كتابة جميع الإعدادات الواحدة تحت الأخرى، تحصل على جدول. و نحصل على الصيغة ${\displaystyle{\displaystyle\varphi_{w}}}$ التي ترمز لوجود جدول رموز محصل عن طريق الإعدادات المتتابعة لحساب مقبول ل w.

إعدادات	0	1	2	3	...	n^k
${\displaystyle{\displaystyle C_{0}=}}$	${\displaystyle{\displaystyle q_{0}}}$	${\displaystyle{\displaystyle W_{1}}}$	${\displaystyle{\displaystyle W_{2}}}$	${\displaystyle{\displaystyle W_{3}}}$	...	#
${\displaystyle{\displaystyle C_{1}=}}$	${\displaystyle{\displaystyle W^{\prime}_{1}}}$	${\displaystyle{\displaystyle q_{1}}}$	${\displaystyle{\displaystyle W_{2}}}$	${\displaystyle{\displaystyle W_{3}}}$	...	#
${\displaystyle{\displaystyle C_{2}=}}$	${\displaystyle{\displaystyle W^{\prime}_{1}}}$	${\displaystyle{\displaystyle W^{\prime}_{2}}}$	${\displaystyle{\displaystyle q_{2}}}$	${\displaystyle{\displaystyle W_{3}}}$	...	#
${\displaystyle{\displaystyle C_{3}=}}$	...	...	...	...	...	#
...	...	...	...	...	...	#
${\displaystyle{\displaystyle C_{n^{k}}}}$	...	...	...	...	...	...

بالنسبة لكل خانة ${\displaystyle{\displaystyle(i,j)\,}}$ من الجدول مع ${\displaystyle{\displaystyle 0\geq i}}$ و ${\displaystyle{\displaystyle j\leq n^{k}}}$ .و كل رمز ${\displaystyle{\displaystyle a\,}}$ ، ندخل المتغير ${\displaystyle{\displaystyle X_{i,j,a}\,}}$ الذي يرمز لكون الخانة تتضمن أو لا الرمز ${\displaystyle{\displaystyle a\,}}$. عدد هذه المتغيرات حدودي.

عندنا العلاقة: ${\displaystyle{\displaystyle\varphi_{w}=\varphi_{cell}\wedge\varphi_{start}\wedge\varphi_{move}\wedge\varphi_{accept}}}$ حيث كل من ${\displaystyle{\displaystyle\varphi_{cell}}}$ و ${\displaystyle{\displaystyle\varphi_{start}}}$ و ${\displaystyle{\displaystyle\varphi_{move}}}$ و ${\displaystyle{\displaystyle\varphi_{accept}}}$ ترمز لوجود مسار مقبول.

الحصول على الصيغة ${\displaystyle{\displaystyle\varphi_{cell}}}$

الصيغة ${\displaystyle{\displaystyle\varphi_{cell}\,}}$ هي صيغة عطف لكل خانة (i,j). و هي تضمن على الأقل أن متغير ${\displaystyle{\displaystyle X_{i,j,a}\,}}$ له القيمة 1 لكن متغيران ${\displaystyle{\displaystyle X_{i,j,a}\,}}$ و ${\displaystyle{\displaystyle X_{i,j,b}\,}}$ لكل ${\displaystyle{\displaystyle a\neq b\,}}$ لا يمكن أن يكون لهما القيمة 1 في نفس الوقت.

الصيغة تكتب على الشكل: ${\displaystyle{\displaystyle\varphi_{cell}=\wedge_{0\leq i,j\leq n^{k}}\left[(\vee_{a\in A}X_{i,j,a})\wedge(\wedge_{a\neq b}\lnot(X_{i,j,a}\wedge X_{i,j,b}))\right]}}$

الحصول على الصيغة ${\displaystyle{\displaystyle\varphi_{start}}}$

تكتب الصيغة هكذا: ${\displaystyle{\displaystyle x_{0,0,q_{0}}\wedge x_{0,1,w_{1}}\wedge x_{0,2,w_{2}}\wedge...\wedge x_{0,n,w_{n}}\wedge x_{0,n+1,D}\wedge...\wedge x_{0,n^{k},D}}}$

مع ملاحظة أن D يرمز ل #.

الحصول على الصيغة ${\displaystyle{\displaystyle\varphi_{accept}}}$

هذه الصيغة تضمن على الأقل أن أحد خانات السطر الأخير من الجدول يضم حالة نهائية.

الصيغة تكتب على الشكل: ${\displaystyle{\displaystyle\varphi_{accept}=\lor_{0\leq j\leq n^{k}}\;and\;{q\in F}\;^{x}\!n^{k},j,q}}$

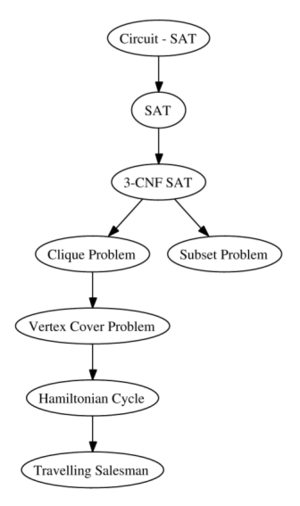
 لائحة ب 21 مسألة NP كلاسيكية (كارب)

المسائل الكلاسيكية

• SATISFIABILITY : الإكتفاء، إيجاد قيم لمتغيرات ثنائية تجعل الصيغة العادية لعطف صحيحة.
• CLIQUE : الزمرة، إيجاد زمرة أي مخطط كامل ذو بعد محدد ضمن مخطط آخر.
• SET PACKING :
• VERTEX COVER : إيجاد ضمن مخطط مجموعة ارتباطات تتصل بكل القمم.
• SET COVERING :
• FEEDBACK ARC SET :
• FEEDBACK NODE SET :
• DIRECTED HAMILTONIAN CIRCUIT : البحث عن مسار هاملتونياني مغلق
• UNDIRECTED HAMILTONIAN CIRCUIT : البحث عن مسار هاملتونياني مفتوح
• 0-1 INTEGER PROGRAMMING :
• 3-SAT : إيجاد قيم لمتغيرات ثنائية تجعل الصيغة العادية لعطف صحيحة تضم كل مجموعة 3 عناصر.
• CHROMATIC NUMBER : تحديد أصغر عدد تلوين مخطط حيث كل قمتين مرتبطتين يكون لهما لونان مختلفان.
• CLIQUE COVER :
• EXACT COVER :
• MATCHING à 3 dimensions :
• STEINER TREE :
• HITTING SET :
• KNAPSACK :
• JOB SEQUENCING :
• PARTITION :
• MAX-CUT :

 أنظر أيضا

• نظرية التعقيد الحسابي.
• مسألة P=NP
• إن بي