216 (عدد)

← 215 216 217 →
← 210 211 212 213 214 215 216 217 218 219 → قائمة الأعداد الأعداد الصحيحة ← 0 100 200 300 400 500 600 700 800 900 →
كمي	صفر
ترتيبي	216 (صفر)
التحليل لعوامل	23× 33
القواسم	1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216
العدد اليوناني	ΣΙϚ´
العدد الروماني	CCXVI
ثنائي	110110002
ثلاثي	220003
رباعي	31204
خماسي	13315
سداسي	10006
ثماني	3308
اثنا عشري	16012
ستة عشري	D816
عشريني	AG20
أساس 36	6036

216 (مئتان وستة عشر) هو عدد طبيعي يلي 215 ويسبق 217. وهو مكعب، وكثيراً ما يُدعى عدد أفلاطون، بالرغم من أنه من غير المؤكد أنه هو العدد الذي كان يقصده أفلاطون.

 في الرياضيات

Visual proof that 3³ + 4³ + 5³ = 6³

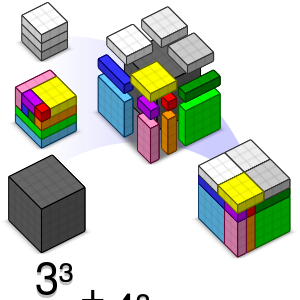
216 is the cube of 6, and the sum of three cubes:

$$216=6^{3}=3^{3}+4^{3}+5^{3}.$$

It is the smallest cube that can be represented as a sum of three positive cubes, making it the first nontrivial example for Euler's sum of powers conjecture. It is, moreover, the smallest number that can be represented as a sum of any number of distinct positive cubes in more than one way. It is a highly powerful number: the product

${\displaystyle{\displaystyle 3\times 3}}$

of the exponents in its prime factorization

${\displaystyle{\displaystyle 216=2^{3}\times 3^{3}}}$

is larger than the product of exponents of any smaller number.

Because there is no way to express it as the sum of the proper divisors of any other integer, it is an عدد غير ملموس. Although it is not a semiprime, the three closest numbers on either side of it are, making it the middle number between twin semiprime-triples, the smallest number with this property. Sun Zhiwei has conjectured that each natural number not equal to 216 can be written as either a triangular number or as a triangular number plus a prime number; however, this is not possible for 216. If the conjecture is true, 216 would be the only number for which this is not possible.

There are 216 ordered pairs of four-element permutations whose products generate all the other permutations on four elements. There are also 216 fixed hexominoes, the polyominoes made from 6 squares, joined edge-to-edge. Here "fixed" means that rotations or mirror reflections of hexominoes are considered to be distinct shapes.

 في المجالات الأخرى

216 هو أحد التفاسير الشائعة لـ عدد أفلاطون، الذي وصفه أفلاطون بتعبيرات غامضة في الجمهورية. Other interpretations include 3600 and 12960000.

There are 216 colors in the web-safe color palette, a ${\displaystyle{\displaystyle 6\times 6\times 6}}$ color cube.

The international calling code for Tunisia

 انظر أيضاً

• قالب:In title