مبرهنة كارنو (نصفا قطر الدائرتين الداخلية والمحيطة)

للاستخدامات الأخرى، انظر مبرهنة كارنو (توضيح)

${\begin{aligned}&DG+DH+DF\\={}&|DG|+|DH|+|DF|\\={}&R+r\end{aligned}}$

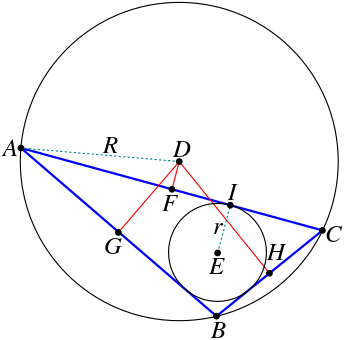
في الهندسة الإقليدية، مبرهنة كارنو Carnot's theorem تنص أن مجموع signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is

$DF+DG+DH=R+r,\$

where r is the inradius and R is the circumradius of the triangle. Here the sign of the distances is taken to be negative if and only if the open line segment DX (X = F, G, H) lies completely outside the triangle. In the diagram, DF is negative and both DG and DH are positive.

المبرهنة مسماة على اسم لازار كارنو (1753–1823). وتُستخدم في إثبات Japanese theorem for concyclic polygons.

 المراجع

• Claudi Alsina, Roger B. Nelsen: When Less is More: Visualizing Basic Inequalities. MAA, 2009, ISBN 978-0-88385-342-9, p.99
• Frédéric Perrier: Carnot's Theorem in Trigonometric Disguise. The Mathematical Gazette, Volume 91, No. 520 (March, 2007), pp. 115–117 (JSTOR)
• David Richeson: The Japanese Theorem for Nonconvex Polygons – Carnot's Theorem. Convergence, December 2013

 وصلات خارجية

• Eric W. Weisstein, Carnot's theorem at MathWorld.
• Carnot's Theorem at cut-the-knot
• Carnot's Theorem by Chris Boucher. The Wolfram Demonstrations Project.