قطعة مستقيمة
| الهندسة |
|---|
 |
| التاريخ (خط زمني) |
| علماء الهندسة |
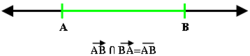
في الهندسة الرياضية،القطعة خط مستقيم (Line segment) تُعرف على أنها جزء من الخط المستقيم محددة بنقطتين تسميان نقطتي النهاية (end points) وتضم جميع النقاط الواقعة على المستقيم بين هاتين النقطتين.
- عندما نقطتي النهاية يحددوا خط منحنى (Curve)،القطعة المستقيمة التي تمر بهما تسمى وتر (Chord).
- عندما نقطتي النهاية ينتمون إلى مضلع،كل قطعة مستقيمة تسمى ضلع إذا تلك النقط هم متجاورتين، وإلا فيسمى قطر (Diagonal).
من الأمثلة على القطع المستقيمة تتضمن أضلاع المستطيل أو المربع.
خصائص
كقطع ناقص مضمحل
A line segment can be viewed as a degenerate case of an ellipse, in which the semiminor axis goes to zero, the foci go to the endpoints, and the eccentricity goes to one. A standard definition of an ellipse is the set of points for which the sum of a point's distances to two foci is a constant; if this constant equals the distance between the foci, the line segment is the result. A complete orbit of this ellipse traverses the line segment twice. As a degenerate orbit, this is a radial elliptic trajectory.
في الأشكال الهندسية الأخرى
In addition to appearing as the edges and diagonals of polygons and polyhedra, line segments also appear in numerous other locations relative to other geometric shapes.
المثلثات
Some very frequently considered segments in a triangle to include the three altitudes (each perpendicularly connecting a side or its extension to the opposite vertex), the three medians (each connecting a side's midpoint to the opposite vertex), the perpendicular bisectors of the sides (perpendicularly connecting the midpoint of a side to one of the other sides), and the internal angle bisectors (each connecting a vertex to the opposite side). In each case, there are various equalities relating these segment lengths to others (discussed in the articles on the various types of segment), as well as various inequalities.
Other segments of interest in a triangle include those connecting various triangle centers to each other, most notably the incenter, the circumcenter, the nine-point center, the centroid and the orthocenter.
رباعيات الأضلاع
In addition to the sides and diagonals of a quadrilateral, some important segments are the two bimedians (connecting the midpoints of opposite sides) and the four maltitudes (each perpendicularly connecting one side to the midpoint of the opposite side).
الدوائر والقطوع الناقصة
Any straight line segment connecting two points on a circle or ellipse is called a chord. Any chord in a circle which has no longer chord is called a diameter, and any segment connecting the circle's center (the midpoint of a diameter) to a point on the circle is called a radius.
In an ellipse, the longest chord, which is also the longest diameter, is called the major axis, and a segment from the midpoint of the major axis (the ellipse's center) to either endpoint of the major axis is called a semi-major axis. Similarly, the shortest diameter of an ellipse is called the minor axis, and the segment from its midpoint (the ellipse's center) to either of its endpoints is called a semi-minor axis. The chords of an ellipse which are perpendicular to the major axis and pass through one of its foci are called the latera recta of the ellipse. The interfocal segment connects the two foci.
قطعة خط موجهة
When a line segment is given an orientation (direction) it is called a directed line segment or oriented line segment. It suggests a translation or displacement (perhaps caused by a force). The magnitude and direction are indicative of a potential change. Extending a directed line segment semi-infinitely produces a directed half-line and infinitely in both directions produces a directed line. This suggestion has been absorbed into mathematical physics through the concept of a Euclidean vector.[1][2] The collection of all directed line segments is usually reduced by making equipollent any pair having the same length and orientation.[3] This application of an equivalence relation was introduced by Giusto Bellavitis in 1835.
تعميمات
Analogous to straight line segments above, one can also define arcs as segments of a curve.
In one-dimensional space, a ball is a line segment.
An oriented plane segment or bivector generalizes the directed line segment.
Beyond Euclidean geometry, geodesic segments play the role of line segments.
A line segment is a one-dimensional simplex; a two-dimensional simplex is a triangle.
أنواع قطع الخطوط
انظر أيضاً
- Polygonal chain
- فترة (رياضيات)
- Line segment intersection, the algorithmic problem of finding intersecting pairs in a collection of line segments
الهامش
- ^ Harry F. Davis & Arthur David Snider (1988) Introduction to Vector Analysis, 5th edition, page 1, Wm. C. Brown Publishers ISBN 0-697-06814-5
- ^ Matiur Rahman & Isaac Mulolani (2001) Applied Vector Analysis, pages 9 & 10, CRC Press ISBN 0-8493-1088-1
- ^ Eutiquio C. Young (1978) Vector and Tensor Analysis, pages 2 & 3, Marcel Dekker ISBN 0-8247-6671-7
المراجع
- ديڤد هيلبرت The Foundations of Geometry. The Open Court Publishing Company 1950, p. 4
